search

fluid boundary

hashtag
概览

当我们在SPHinXsys中设定一个流体边界时，通常要同时指定两类东西：

  1. 这是一个入口还是出口？或者既可以流入又可以流出？

  2. 设定边界压力还是速度？

据此将流体边界分为两大类：

  1. 第一类是buffer，buffer是一个入口或出口的缓冲区（通常是AlignedBox）。通过body part机制只遍历该区域对应的粒子；对速度边界，通常是在该区域内对粒子速度做“松弛/投影”；对开边界（inflow/outflow），通常还要配合粒子注入/删除，并配套预留buffer particle内存。单向buffer包括用于流入的EmitterInflowInjection、用于流出的DisposerOutflowDeletion和既可流入又可流出的BidirectionalBuffer。

  2. 第二类用于设定粒子的属性。包括设定速度的InflowVelocityCondition、TargetVelocity和设定压力的PressureBoundaryCondition、TargetPressure。

本文聚焦几个最常用的边界机制，源码主要位于src\shared\particle_dynamics\fluid_dynamics\boundary_condition\fluid_boundary.h/.cpp和src\shared\particles\particle_reserve.h/.cpp。这里我们关心如何在底层上实现，而不是如何使用。关于使用，请移步案例注解arrow-up-right。

注意区分本文的两个概念：buffer区域的粒子和buffer particle。前者指的是位于buffer区域（某个aligned box）的粒子，属于real particle。后者指的是内存空间中预留的空位置，属性没有任何意义，不属于real particle。

hashtag
速度边界：InflowVelocityCondition

类模板fluid_dynamics::InflowVelocityCondition<TargetVelocity>定义于fluid_boundary.h。它的特点是：

  • body part类型是AlignedBoxByCell，即按空间区域施加；

  • 对box内粒子直接修改速度；

  • 支持松弛率relaxation_rate（默认1.0表示完全强制到目标速度）。

hashtag
TargetVelocity接口

TargetVelocity应当是一个函数对象，签名为：

注意这里的position/velocity是在aligned box的local frame下（源码会用Transform把base frame转换到frame）。因此TargetVelocity里写抛物线剖面/泊肃叶剖面时，通常以“box的对齐轴方向”为入口方向。

TargetVelocity一般由用户自定义，如tests\2d_examples\test_2d_channel_flow_fluid_shell\channel_flow_shell.cpp中的InflowVelocity。

hashtag
update逻辑（源码级）

update(index_i)的逻辑非常直接：

  1. 若粒子位于box内（aligned_box_.checkContain(pos_[index_i])），则将其位置/速度转换到local frame；

  2. 调用target_velocity(frame_position, frame_velocity, physical_time)得到目标速度；

  3. 用relaxation_rate做线性松弛： un+=αutarget+(1−α)un\mathbf{u}^{n+}=\alpha\mathbf{u}_{\mathrm{target}}+(1-\alpha)\mathbf{u}^{n}

  4. 再把速度变换回base frame写回。

补充：InflowVelocityCondition只改速度，不会同步修正压力/密度/力，因此更像一个“速度投影/约束”算子。对开边界场景，通常放在声学子步末尾更稳定（见03案例中的试验讨论）。

hashtag
流入边界：EmitterInflowInjection

类fluid_dynamics::EmitterInflowInjection定义于fluid_boundary.h，实现在fluid_boundary.cpp。它用于开边界的粒子注入：当emitter区域的某个粒子越过aligned box的upper bound时，创建一个新的real particle，并把越界粒子周期映射回emitter的lower side附近。

hashtag
构造与依赖

构造函数签名：

要点：

  • emitter必须是AlignedBoxByParticle：保证遍历集合稳定，不会因为粒子跑出box就失去遍历机会。

  • 必须传入ParticleBuffer并且已reserve，否则checkParticlesReserved()会直接报错退出。

hashtag
original id与sorted id

注入update的形参是original_index_i，实现里会做一次映射：

原因是：

  • AlignedBoxByParticle在tag时记录的是“当时的粒子索引”，这更接近original id语义；

  • 但粒子属性数组在很多配置里会按sorted顺序存取（粒子排序后），因此需要用SortedID把original id映射到当前的sorted index。

hashtag
update逻辑

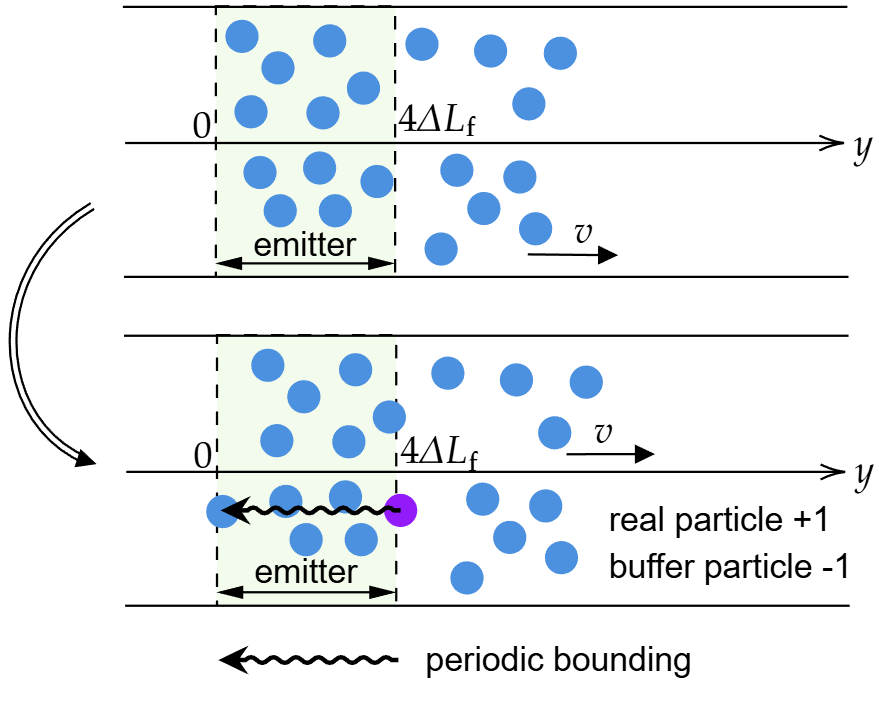
EmitterInflowInjection::update做了两件事：

  1. 检测是否越过upper bound：

  • 若aligned_box_.checkUpperBound(pos_[sorted_index_i])为真，则进入注入。

  1. 在互斥锁保护下把一个buffer particle转为real particle：

  • buffer_.checkEnoughBuffer(*particles_)确保容量足够；

  • particles_->createRealParticleFrom(sorted_index_i)在数组尾部创建一个新real particle，并复制越界粒子状态。

  1. 把旧粒子做periodic bounding并重置为参考态：

  • pos_[sorted_index_i]=aligned_box_.getUpperPeriodic(pos_[sorted_index_i])；

  • rho_设为参考密度，p_由状态方程重算。

直观理解就是：越界粒子“吐出”一个拷贝作为新注入粒子；自己则被“卷回”入口端，作为后续持续注入的供体。

互斥锁的意义是：注入通常可能在并行遍历中执行，创建/切换粒子状态涉及修改TotalRealParticles()等全局计数，必须保证线程安全。

补充：同文件里还有EmitterInflowCondition，它用于“随emitter运动的入口条件”（会基于old/new transform更新粒子位置/速度，并把密度压力重置到入口参考态）。它同样依赖AlignedBoxByParticle，但侧重点是“入口本身在动”。

hashtag
流出边界：DisposerOutflowDeletion

类fluid_dynamics::DisposerOutflowDeletion定义于fluid_boundary.h，实现在fluid_boundary.cpp。它用于将越过aligned box upper bound的粒子从real particle集合中删除（切回buffer particle）。

hashtag
构造与遍历方式

构造函数签名：

它使用AlignedBoxByCell，即遍历的是disposer区域当前cell中的粒子（sorted index语义），所以update里直接用index_i访问pos_，不需要做sorted id映射。

hashtag
为什么是while而不是if

源码逻辑：

这里必须用while而不是if，原因与switchToBufferParticle的“与最后一个real particle交换/覆盖”的删除策略有关：

  • 假设index_i处粒子越界，删除时会把最后一个real particle的状态拷贝/交换到index_i；

  • 若被换进来的那个粒子同样越界，那么只做一次if会漏删；

  • while会继续检查当前index_i处“新换进来的粒子”，直到该位置不再越界或index_i已经落在real particle范围之外。

同时需要index_i < TotalRealParticles()这个条件：因为删除会动态减少real particle数量，而body part的loop range并不会在此处同步缩小，后续仍可能遍历到“已变成buffer particle的索引”，该判断可以避免误删/越界访问。

hashtag
流入/流出双向buffer

在定常速度边界中，buffer区域通常是单向的入口或出口。压力边界就不一样了，流体可以从buffer一端进入流体内部区域，也可以从buffer另一端流出bounding box。为了实现这个特性，SPHinXsys定义了类BidirectionalBuffer，位于tests\extra_source_and_tests\extra_src\shared\pressure_boundary\bidirectional_buffer.h。可想而知，这个类需要满足以下特性：

注意双向buffer中“注入/删除”对应的是box两端：Injection通常在upper bound一侧触发（粒子从upper端流出buffer，周期映射回lower端并注入一个新real particle），Deletion通常在lower bound一侧触发（粒子从lower端流出buffer即删除）。具体以aligned box对齐轴方向为准。

  • 能够管理buffer区域的粒子，实现动态标记；

  • 当流体粒子从buffer区域一端流入流体内部时，将此粒子注入（一个buffer particle转为real particle）

  • 当流体粒子从buffer区域另一端流出计算域时，将此粒子删除（一个real particle转为buffer particle）

下图是原始论文bidirectional buffer的解释（Zhang et al, 2025）：

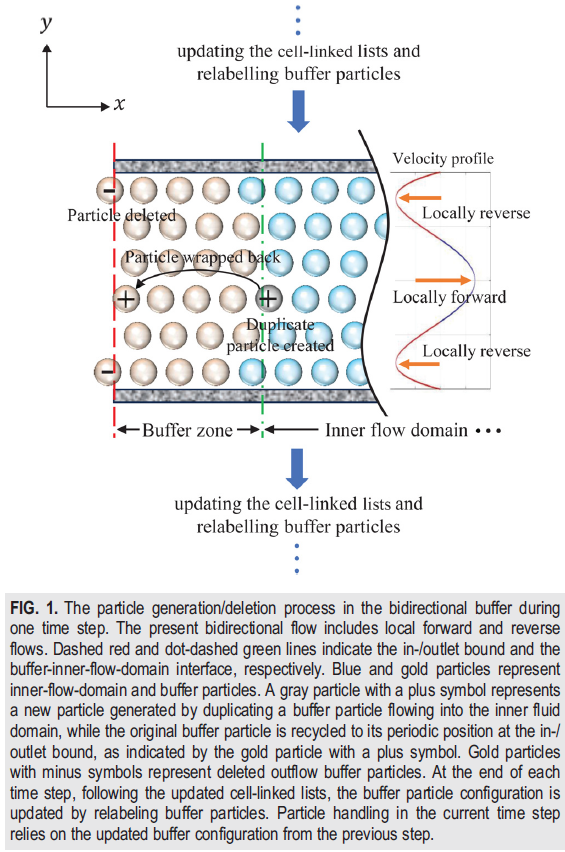
BidirectionalBuffer的设计就是按照这三个特性来的：

它具有三个嵌套类和由这三个类衍生出的SimpleDynamics成员，分别实现上述三个特性。在构造时接收一个aligned_box_part对象作为buffer区域（三个成员都要用），接收一个ParticleBuffer<Base>对象传递给injection成员。此外，它还有一个TargetPressure（模板参数，可为NonPrescribedPressure或类似的用户自定义类）类型。

hashtag
动态标记类

part_id_是每个body part独有的ID。buffer_indicator_表明某个粒子属于哪个buffer区域（0代表内部流动区，1及以上代表buffer）。update函数中，如果某个粒子在aligned box范围内，就将其buffer_indicator_置为part_id_。

hashtag
注入类

upper_bound_fringe_是留给aligned box右边界的裕度，设为0.5ΔL0.5\Delta L。如果一个粒子同时满足以下三个条件：

  1. 在轴线上的坐标超过了右边界+0.5ΔL0.5\Delta L；

  2. 它在上一个时间步属于这个buffer区域

  3. 它是real particle（感觉这个判断也有点多余，如果不是real particle的话就几乎不会被遍历到了）

那么就基于此粒子，原位拷贝出一个新real particle（将一个buffer particle转为real particle），将这个新的real particle的buffer_indicator_置为0（内部流动区域）。然后再对原粒子做periodic bounding，其压力设为target pressure，密度由target pressure计算出。另外要把原粒子的previous_surface_indicator_置为1，这是为了确保这个映射回左边界的粒子能够被识别为自由表面的粒子（算法中如果一个粒子在上一个时间步不是自由表面粒子，那么在本时间步就会倾向于把它判定为体相粒子）。

hashtag
删除类

在update函数中，如果一个粒子同时满足以下三个条件：

  1. 超出了左边界

  2. 在上一个时间步属于这个buffer区域

  3. 是real particle

那么就将其删除（转为buffer particle）。

hashtag
压力边界：PressureBoundaryCondition

类比于指定速度边界时我们需配合使用InflowVelocityCondition和TargetVelocity，在指定压力边界时，我们需要配合使用PressureBoundaryCondition和TargetPressure。

hashtag
TargetPressure接口

TargetPressure应当是一个函数对象，签名为：

源码中提供的是NonPrescribedPressure，即不指定压力。用户可以自定义，如tests\extra_source_and_tests\test_2d_pulsatile_poiseuille_flow\pulsatile_poiseuille_flow.cpp中的LeftInflowPressure和RightInflowPressure。

hashtag
压力边界

hashtag
理论

为了使得内部流动区域的流体粒子具有完整的支撑域，buffer区域至少要有三层粒子。可是buffer区域边缘的粒子就没办法保证有完整的支撑域了。然而边界的流速计算依赖于压力梯度的计算（动量方程），所以“如何使得边界上没有完整支撑域的粒子也能计算出正确的压力梯度”就是个要重点解决的问题，也是Zhang et al（2025）主要解决的问题。在其论文中，假想buffer区域之外有一堆粒子，如果这些假想的粒子存在，那么buffer区域的粒子的支撑域就完整了。可这些假想粒子实际上是缺失的。作者通过一些巧妙的数学变换，使得在这些粒子缺失的情况下也能正确考虑它们的影响。

首先，根据梯度的反对称性，有以下近似（前提是粒子均匀分布）：

∑jmjρj∇Wij≈0.\sum_j \frac{m_j}{\rho_j}\nabla W_{ij}\approx \boldsymbol{0}.

对buffer区域的粒子来说，如果算上边界外缺失的粒子，那么上式依然成立。我们记buffer区域的粒子下标为jj，缺失粒子的下标为kk，于是

∑jmjρj∇Wij+∑kmkρk∇Wik≈0.\sum_j \frac{m_j}{\rho_j} \nabla W_{i j}+\sum_k \frac{m_k}{\rho_k} \nabla W_{i k} \approx \boldsymbol{0}.
∑kmkρk∇Wik≈−∑jmjρj∇Wij.(1)\sum_k \frac{m_k}{\rho_k} \nabla W_{i k}\approx -\sum_j \frac{m_j}{\rho_j} \nabla W_{i j}.\tag{1}

SPHinXsys使用Riemann solver进行物理场的稳定。对于buffer区域粒子，带有Riemann solver的压力梯度离散形式为

∇pi=2∑jPij∗mjρj∇Wij+2∑kPik∗mkρk∇Wik,\nabla p_i=2 \sum_j P_{i j}^* \frac{m_j}{\rho_j} \nabla W_{i j}+2 \sum_k P_{i k}^* \frac{m_k}{\rho_k} \nabla W_{i k},

其中P∗P^*是任意两个粒子对的压力Riemann solution。

对于边界外的粒子，我们指定它具有恒定的压力pbp_\mathrm{b}（第一类边界条件），也即Pik∗=pbP_{i k}^*=p_\mathrm{b}。结合式(1)，可以得出

∇pi=2∑jPij∗mjρj∇Wij−2pb∑jmjρj∇Wij.\nabla p_i=2 \sum_j P_{i j}^* \frac{m_j}{\rho_j} \nabla W_{i j}-2 p_\mathrm{b} \sum_j \frac{m_j}{\rho_j} \nabla W_{i j} .

将其代入动量方程的离散形式：

dvidt=−2∑jmj(Pij∗ρiρj)∇Wij+2pb∑j(mjρiρj)∇Wij+2∑jmjηvijρiρjrij∂Wij∂rij+g.(2)\begin{aligned} \frac{d \mathbf{v}_i}{d t}= & -2 \sum_j m_j\left(\frac{P_{i j}^*}{\rho_i \rho_j}\right) \nabla W_{i j}+2 p_\mathrm{b} \sum_j\left(\frac{m_j}{\rho_i \rho_j}\right) \nabla W_{i j} \\ & +2 \sum_j m_j \frac{\eta \mathbf{v}_{i j}}{\rho_i \rho_j r_{i j}} \frac{\partial W_{i j}}{\partial r_{i j}}+\mathbf{g} . \end{aligned}\tag{2}

注意，动量方程中多出的一项是PressureBoundaryCondition干的第一件事（也是最重要的）：

2pb∑j(mjρiρj)∇Wij2 p_\mathrm{b} \sum_j\left(\frac{m_j}{\rho_i \rho_j}\right) \nabla W_{i j}

它干的第二件事，是令速度只有边界的法向分量，没有切向分量，也就是做了个投影：

vi=(vi⋅u^)u^,\mathbf{v}_i=\left(\mathbf{v}_i \cdot \hat{u}\right) \hat{u},

其中u^\hat{u}是buffer区域边界的单位法向量。

hashtag
实现

构造函数接收一个AlignedBoxByCell对象，从中获取aligned box、轴线方向和变换，初始化了kernel_sum_。这里kernel_sum_就是∑j(mj/ρj)∇Wij\sum_j (m_j/\rho_j)\nabla W_{ij}。update函数中，如果粒子位于aligned box之内，那么依次执行

  1. 速度递增2pb∑jmj/(ρiρj)∇Wij2 p_\mathrm{b} \sum_j m_j/(\rho_i \rho_j) \nabla W_{i j}，如需要修正核函数梯度，施加之；

  2. 只保留速度的法向分量。这里有三行代码，看着多，实际上是为了处理有旋转变换的情况（aligned box与坐标轴不对齐）。

调用时，可以根据是否需要修正核梯度，调用以下两个别名：

hashtag
参考文献

Zhang S., Fan Y., Wu D., Zhang C., Hu X.; Dynamical pressure boundary condition for weakly compressible smoothed particle hydrodynamics. Physics of Fluids 2025; 37 (2): 027193. https://doi.org/10.1063/5.0254575

Previousdensity summationNextfluid integration

Last updated